Формат ПОЛЬЗОВАТЕЛЬСКОГО СКРИПТА ДЛЯ ОТОБРАЖЕНИЯ ФОРМУЛ: http://eek.diary.ru/ C1 Критерии:
2 б. - Обоснованно получен правильный ответ
1 б. - Получен ответ, но решение неверно только из-за того, что не учтены ограничения на знак или величину выражения cosx (sinx)
0 б. - Решение не соответствует ни одному из критериев, перечисленных выше
(вар. 148 Запад)
Решите систему уравнений `{(y+cosx=0),((2sqrt(cosx)-1)(7y-6)=0):}` Ответ: `(pm arccos (1/4) + 2pin; -1/4), n in ZZ`
Решение:
Из второго уравнения получаем: `{(y=6/7),(cosx ge 0):}` или `cosx=1/4`.
Если `y=6/7`, то из первого уравнения `cosx = -6/7`. Это противоречит условию `cosx ge 0`.
Если `cosx=1/4`, то `x=pm arccos(1/4)+2pin, n in ZZ`, и из первого уравнения получаем: `y=-1/4`.
C2 Критерии:
2 б. - Обоснованно получен правильный ответ
1 б. - Способ нахождения искомого угла верен, но получен неверный огвет или решение не закончено
0 б. - Решение не соответствует ни одному из критериев, перечисленных выше
(вар. 148 Запад), (вар. 112 Запад), (вар. 190 Запад)
В правильной треугольной пирамиде `SABC` с основанием `ABC` известны ребра: `AB=12sqrt3, SC=13`. Найдите угол, образованный плоскостью основания и прямой `AM` , где `M` - точка пересечения медиан грани `SBC`. Ответ: `arctg 5/48`
Решение:
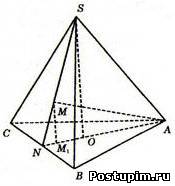Пусть `N` - середина `BC`. Прямая `NS` проектируется на плоскость основания в прямую `AN`. Поэтому проекция точки `M` - точка `M_1` лежит на отрезке `AN`. Значит, прямая `AN` является проекцией прямой `AM`, следовательно угол `MAM_1` - искомый.
`MM_1 || SO`, где `O` - центр основания, значит, треугольники `SNO` и `MNM_1` подобны с коэффициентом 3.
Тогда `AM_1=AN-NM_1=AN-1/9 AN=8/9AN=16`. Кроме того, `MM_1=1/3SO=1/3sqrt(SC^2-CO^2)=5/3`.
Из прямоугольного треугольника `MM_1A` находим: `tg /_MAM_1 = {MM_1}/{AM_1}=5/48`. Значит искомый угол равен `acrtg 5/48`.
(вар. 128 Запад)
В правильной треугольной пирамиде `SABC` с основанием `ABC` известны ребра: `AB=20sqrt3, SC=29`. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер `AS` и `BC`. Ответ: `arctg 21/40`
Решение:
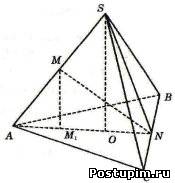Пусть `M` и `N`середины ребер `AS` и `BC` соответственно. Прямая `AS` проектируется в прямую `AN`. Поэтому проекция точки `M` - точка `MM_1` - лежит на отрезке `AN`. Значит, прямая `AN` является проекцией прямой `MN`, следовательно, угол `MNM_1` - искомый.
`MM_1 || SO`, где `O` - центр основания, значит, `MM_1` - средняя линия треугольника `ASO`, а поэтому `M_1` - середина `AO`. Тогда `AM_1=1/3AN=10` и `M_1N=2/3AN=20`.
Из прямоугольного треугольника `AM_1M` находим: `MM_1=sqrt(AM^2-AM_1^2)=sqrt(841/4-100)=21/2`.
Из прямоугольного треугольника `MM_1N` находим: `tg /_ MNM_1 = {MM_1}/{M_1N} = 21/40`.
Значит искомый угол равен `acrtg 21/40`.
C3 Критерии:
3 б. - Обоснованно получен правильный ответ
2 б. - Обоснованно получен ответ, отличающийся от верного только конечным числом точек
1 б. - Полученный ответ неверен, но решение содержит переход от исходного неравенства к верным рациональным неравенствам
0 б. - Решение не соответствует ни одному из критериев, перечисленных выше
(вар. 148 Запад), (вар. 112 Запад)
Решите неравенство: `log_5((7^{-x^2}-5)(7^{-x^2+16}-1))+log_5({7^{-x^2}-5}/{7^{-x^2+16}-1})>log_5(7^{2-x^2}-1)^2`
Ответ: `(-oo;-4) uu (4;+oo)`
Решение:
Пусть `t=7^{-x^2}, 0 lt t le 1`, тогда неравенство принимает вид: `log_5((t-5)(7^16t-1))+log_5({t-5}/{7^16t-1})>log_5(7^2t-1)^2`.
`t-5 lt 0`, поэтому `7^16t-1 lt 0`, то есть `0 lt t lt 1/7^16`.
Получаем: `{(log_5(t-5)^2 gt log_5(49t-1)^2),(0 lt t lt 1/7^16):} \ iff {(|t-5| gt |49t-1|),(0 lt t lt 1/7^16):} \ iff {(5-t gt 1-49t),(0 lt t lt 1/7^16):} \ iff 0 lt t lt 1/7^16`.
Тогда `7^{-x^2} lt 7^-16 iff x^2 gt 16 iff x in (-oo; -4) uu (4; +oo)`
>( 
:'( 
RSS:
