|
Задания реальнных КИМов
| |
| admin | Дата: Четверг, 2012-06-07, 3:21 AM | Сообщение # 16 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| C2 В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 1, боковые ребра равны 2. Точка E - середина ребра AA1. Найдите расстояние от вершины A до плоскости BED1.
C2 В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые ребра 3. Точка E - середина ребра AA1, Найдите расстояние от вершины A до плоскости BED1.
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 3:22 AM | Сообщение # 17 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| C3 Решите систему неравенств.
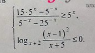
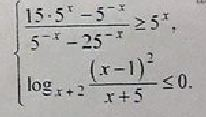
РЕШЕНИЕ:
(15*5^x-5^(-x))/(5^(-x)-25^(-x))>=5^x
log_(x+2)(x-1)^2/(x+5)<=0
1) (15*5^x-5^(-x))/(5^(-x)-25^(-x))>=5^x
ОДЗ
5^(-x)-25^(-x)!=0 ; x!=0
Замена 5^x=t ; t>0
(15t-1/t)/(1/t-1/t^2)>=t
((15t^2-1)t^2)/(t(t-1))>=t
(15t^3-t)/(t-1)-t>=0
(15t^3-t-t^2+t)/(t-1)>=0
(t^2(15t-1))/(t-1)>=0
15t-1=0 ; t=1/15
t-1!=0 ; t!=1
t<=1/15 ; t>1
5^x<=1/15
log_5 5^x<=log_5 (5^(-1)*3^(-1))
x<=-1-log_5 3
5^x>1
5^x>5^0
x>0
2) log_(x+2)(x-1)^2/(x+5)<=0
ОДЗ
x+2>0 , x>-2
x+2!=1 , x!=-1
x!=1
x> -5
x in (-2;-1)uu(-1;1)uu(1;+oo)
Применим метод рационализации
(x+2-1)((x-1)^2/(x+5)-1)<=0
(x+1)(x^2-2x+1-x-5)/(x+5)<=0
(x+1)(x^2-3x-4)/(x+5)<=0
((x+1)(x+1)(x-4))/(x+5)<=0
x in (-2;-1)uu(-1;1)uu(1;4]
Найдем решение системы
x in (-2;-1-log_5 3]uu(0;1)uu(1;4]
Ответ: x in (-2;-1-log_5 3]uu(0;1)uu(1;4]
C3 Решите систему неравенств
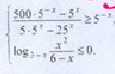
РЕШЕНИЕ:
C3.
(500*5^(-x) -5^x)/ (5*5^x – 25^x) >= 5^(-x)
log_(3-x) (x^2 / (6-x)) <=0
log_(3-x) (x^2 / (6-x)) <=0
ОДЗ.
3 – x >0
3 – x != 1
X != 0
6 – x > 0
=>ОДЗ x in (-oo, 0) u (0;2) u (2;3)
Это уравнение на ОДЗ эквивалентно следующему:
( 3 – x – 1) ( x^2 / (6-x) – 1) <=0
(2-x) (x^2 + x - 6) <=0
(2-x) (x - 2)(x + 3) <= 0
(x-2)^2 (x+3) >=0
=> x in [-3;0) u (0;2)u(2;3)
Итого: решение второго уравнения: x in [-3;0) u (0;2) u (2;3).
(500*5^(-x) -5^x)/ (5*5^x – 25^x) >= 5^(-x)
(500*5^(-2x) -1)/ (5 – 5^x) - 5^(-x) >= 0
(- 5*5^(-x) + 500 * 25^(-x) ) / ( 5 – 5^x) >=0
5^(-x) (100*5^(-x) -1)/ (5 – 5^x) >= 0
Это неравенство эквивалентно (x = 1 не решение)
(100*5^(-x) -1)* (5 – 5^x) >= 0
=> x in (-oo;1) u [ 2 + log_5 4; +oo)
Ответ: x in [-3;0) u (0;1) u (2; 2 + log_5 4).
С3 Решите систему неравенств:
(36 - 9^x)/(9 - 3^x) >= 4
log_x^2 (2-x) <= 1
РЕШЕНИЕ:
(36 - 9^x)/ ( 9 - 3 ^ x) >= 4
log_(x^2) (2 - x) <= 1
(36 - 9^x)/ ( 9 - 3 ^ x) >= 4
(36 - 9^x)/ ( 9 - 3 ^ x) - 4 >= 0
(-9^x +4*3^x) / ( 9 - 3^x) >= 0
3^x = t >0
(-t^2 + 4t)/ ( 9 - t) >=0
Это эквивалентно следующей системе:
(-t^2 + 4t) (9 - t) >= 0
t != 9
t ( 4 - t) (9 - t) >= 0 <=> (4 - t)(9 - t) >= 0 <=> t in (0; 4] u (9; +oo)
<=> x in (-oo; log_3 4] u (2; + oo)
log_(x^2) (2 - x) <= 1
ОДЗ.
x^2 != 0; 1
2 - x > 0
Это неравенство на ОДЗ эквивалентно следующему неравенству:
( x ^ 2 - 1) ( 2 - x - x^2) <= 0
(x-1)(x+1)( 1 - x)(2 + x) <=0
(x - 1 )^2 (x + 1) ( 2 + x) >= 0
x in (-oo;-2] uuu (-1;0)u(0;1)u(1;2)
Объединяем решения и поkучаем:
Ответ: ( -oo; -2] u(-1;0) u (0;1) u (1; log_3 4).
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 3:22 AM | Сообщение # 18 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| C4 В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что радиус окружности, касающейся стороны треугольника и продолжений двух других его сторон, в 7 раз больше радиуса вписанной окружности?
C4 В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других сторон, равно 2/7?
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 3:22 AM | Сообщение # 19 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| C5 Найдите все значение а, при каждом из которых уравнение
ax-2=|5/x - 3|
на промежутке от (0;+oo) имеет ровно 1 корень.
C5 Найдите все значения a, при каждом из которых уравнение ax-1=|5/x-4| на промежутке (0;+inf) имеет ровно один корень.
РЕШЕНИЕ:
C5.
ax-1=|5/x - 4| - единственный положительный корень.
ОДЗ: ax-1>=0
ax>=1.
Если a=0 - решений нет.
Если a<0: x<=1/a - ОДЗ полностью отрицательное, положительных решений быть не может.
Если a>0: x>=1/a - ОДЗ.
Получаем совокупность двух уравнений:
ax-1=+-(5/x - 4)
Первое уравнение: ax-1=5/x -4
(ax^2+3x-5)/x=0
ax^2+3x-5=0
можем умножить на x, лишние корни не появятся, т.к. по ОДЗ x всегда положительный.
Дискриминант D=9+20a>0 при всех наших положительных a, поэтому уравнение всегда имеет два корня, при этом их произведение по т. Виета = -5/a < 0, поэтому один из корней положительный, другой отрицательный.
Один положительный корень уже есть, поэтому второе уравнение не должно иметь положительных решений.
Второе уравнение:
ax-1=-5/x +4,
ax^2-5x+5=0,
D=25-20a.
Если D<0 - то все ок, уравнение не имеет корней, поэтому a>5/4 идет в ответ.
Пусть a<=5/4, тогда уравнение имеет корни, но по Т. Виета их сумма и произведение положительны, поэтому оба корня положительны, т.е. не выполняется исходное условие задачи.
Ответ: a>5/4.
С5

РЕШЕНИЕ:
С5
ax-1=|6/x - 5| - единственный положительный корень.
ОДЗ: ax-1>=0
ax>=1.
Если a=0 - решений нет.
Если a<0: x<=1/a - ОДЗ полностью отрицательное, положительных решений быть не может.
Если a>0: x>=1/a - ОДЗ.
Получаем совокупность двух уравнений:
ax-1=+-(6/x - 5)
Первое уравнение: ax-1=6/x -5
(ax^2+4x-6)/x=0
ax^2+4x-6=0
можем умножить на x, лишние корни не появятся, т.к. по ОДЗ x всегда положительный.
Дискриминант D=16+24a>0 при всех наших положительных a, поэтому уравнение всегда имеет два корня, при этом их произведение по т. Виета = -6/a < 0, поэтому один из корней положительный, другой отрицательный.
Один положительный корень уже есть, поэтому второе уравнение не должно иметь положительных решений.
Второе уравнение:
ax-1=-6/x +5,
ax^2-6x+6=0,
D=36-24a.
Если D<0 - то все ок, уравнение не имеет корней, поэтому a>3/2 идет в ответ.
Пусть a<=3/2, тогда уравнение имеет корни, но по Т. Виета их сумма и произведение положительны, поэтому оба корня положительны, т.е. не выполняется исходное условие задачи.
Ответ: a>3/2.
Теперь рассмотрим тот случай, когда положительный корень первого уравнения не удовлетворяет ОДЗ, графически это означает, что f(1/a)>0, т.е. правый корень находится левее точки 1/a. Подставим: 1/a+4/a-6>0,
5/a>6
a<5/6.
Тогда второе уравнение должно иметь ровно 1 положительный корень, удовлетворяющий ОДЗ.
При таких a оно имеет два корня, поэтому, графически, точка 1/a должна оказаться между ними.
Иначе говоря, g(1/a)<=0.
Подставим: 1/a-6/a+6<=0,
5/a>=6,
a<=5/6.
В пересечении получилось, что a<5/6, т.е. особая точка a=5/6, при которой и меньший корень мог совпать с 1/a, что дало бы нам 2 корня - отпал.
Ответ: a принадлежит (0;5/6)U(3/2;+oo)
С5

РЕШЕНИЕ:
ax-2=|5/x - 3| - единственный положительный корень.
ОДЗ: ax-2>=0
ax>=2.
Если a=0 - решений нет.
Если a<0: x<=2/a - ОДЗ полностью отрицательное, положительных решений быть не может.
Если a>0: x>=2/a - ОДЗ.
Получаем совокупность двух уравнений:
ax-2=+-(5/x - 3)
Первое уравнение: ax-2=5/x -3
(ax^2+x-5)/x=0
ax^2+x-5=0
можем умножить на x, лишние корни не появятся, т.к. по ОДЗ x всегда положительный.
Дискриминант D=1+20a>0 при всех наших положительных a, поэтому уравнение всегда имеет два корня, при этом их произведение по т. Виета = -5/a < 0, поэтому один из корней положительный, другой отрицательный.
Один положительный корень уже есть, поэтому второе уравнение не должно иметь положительных решений.
Второе уравнение:
ax-2=-5/x +3,
ax^2-5x+5=0,
D=25-20a.
Если D<0 - то все ок, уравнение не имеет корней, поэтому a>5/4 идет в ответ.
Пусть a<=5/4, тогда уравнение имеет корни, но по Т. Виета их сумма и произведение положительны, поэтому оба корня положительны
Теперь рассмотрим тот случай, когда положительный корень первого уравнения не удовлетворяет ОДЗ, графически это означает, что f(1/a)>0, т.е. правый корень находится левее точки 2/a. Подставим: 4/a+2/a-5>0,
6/a>5
a<6/5.
Тогда второе уравнение должно иметь ровно 1 положительный корень, удовлетворяющий ОДЗ.
При таких a оно имеет два корня, поэтому, графически, точка 2/a должна оказаться между ними.
Иначе говоря, g(2/a)<=0.
Подставим: 4/a-10/a+5<=0,
6/a>=5,
a<=6/5.
В пересечении получилось, что a<6/5, т.е. особая точка a=6/5, при которой и меньший корень мог совпать с 2/a, что дало бы нам 2 корня - отпал.
Ответ: a принадлежит (0;6/5)U(5/4;+oo)
С5 Найдите все значения а, при каждом из которых уравнение
|5/x - 3| = ax - 1
на промежутке (0; +беск) имеет более двух корней
РЕШЕНИЕ:
|5/x -3|=ax-1 - больше двух положительных решений.
ОДЗ: ax>=1.
a=0 - решений нет.
a<0: x<=1/a<0 - положительных решений быть не может.
a>0: x>=1/a.
Получаем совокупность двух уравнений
5/x-3=ax-1
3-5/x=ax-1
Приведем к общему знаменателю, умножим на x, имеем право, корни не приобретем, по ОДЗ x>=1/a>0.
ax^2+2x-5=0
ax^2-4x+5=0
В совокупности эти уравнения должны иметь минимум три решения, удовлетворяющие условию x>=1/a.
У первого уравнения произведение корней -5/a<0, поэтому может быть только 1 положительное решение.
Значит, второе уравнение должно иметь 2 корня >=1/a, в первое уравнение должно иметь 1 корень >=1/a, при этом корни не должны совпадать.
Оба дискриминанта должны быть положительными,
D_1=4+20a>0 - при всех a>0
D_2=16-20a>0 => a<4/5.
Корень первого уравнения >=1/a если f(1/a)<=0 - необходимое и достаточное условие.
1/a+2/a-5<=0, 3/a<=5, a>=3/5.
Оба корня второго уравнения по Т. виета положительны, поэтому они будут лежать правее точки 1/a если g(1/a)>=0.
1/a-4/a+5>=0, a>=3/5.
Заметим, что при a=3/5 - корни обоих уравнений совпадают, значит эту точку выкидываем. При других a совпадений корней нет - легко проверить, сказав, что у уравнений
5/x-3=ax-1
3-5/x=ax-1
есть общий корень, получаем, что только при a=3/5.
Также, вершина второй параболы должна лежать правее точки 1/a,
т.е. 2/a>1/a - всегда верно при положительных a.
Ответ: 3/5
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 3:23 AM | Сообщение # 20 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| C6 Имеется 33 коробки массой 19 кг каждая и 27 коробок массой 49 кг каждая. Все эти коробки раскладывают по двум контейнерам. Пусть S - модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S:
a)если дополнительно требуется, что в контейнерах должно находится одинаковое количество коробок;
b)без дополнительного условия пунка a.
C6 Имеется 17 коробок массой 37 кг и 25 коробок массой 61 кг каждая. Все эти коробки раскладывают по двум контейнерам. Пусть S - модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S:
a)если дополнительно требуется, что в контейнерах должно находится одинаковое количество коробок;
b)без дополнительного условия пункта a.
РЕШЕНИЕ:
a. Пусть a - количество 37кг коробок в 1 контейнере, тогда 17-a - кол-во 37 кг. коробок во 2 контейнере.
Также, в силу того, что в каждом контейнере по 21 коробке, получаем, что в 1 контейнере 21-a коробок весом 61кг и следовательно во втором контейнере 25-(21-a)=4+a коробок весом 61 кг.
Массая первого контейнера m_1=37a+61(21-a), второго контейнера
m_2=37(17-a)+61(4+a).
Тогда, модуль нашей разности суммарных масс контейнеров равен
d=|m_2 - m_1|=|61(2a-17)-37(2a-17)|=24*|2a-17|.
a - целое, поэтому 2a-17 - нечетное число, следовательно |2a-17|>=1.
Значит d>=24. При этом равенство достигается при a=8 или 9.
d_min=24.
b. x - количество 37кг коробок в 1 контейнере, y - кол-во 61 кг. коробок в 1 контейнере. Тогда 17-x и 25-y - кол-ва коробок во втором контейнере.
d=|(2x-17)*37+(2y-25)*61|=2|37x+61y-1077|.
Предположим, что найдутся такие целые x,y, при этом x принимает значения от 0 до 17, y принимает значения от 0 до 25, что d=0,
т.е. 37x+61y=1077.
61(x+y)=1077+24x,
1077+24x делится на 61,
-21+24x делится на 61.
3(8x-7) делится на 61
8x-7 делится на 61,
но -7<=8x-7<=129, значит может равняться либо 0, либо 61, либо 122,
в каждом из этих случаев получаем противоречие.
Значит выражение |37x+61y-1077| минимально может равняться 1, при этом оно равно 1 при x=6, y=14.
Ответ: a. 24
b. 2
C6 Имеется 27 коробок массой 17 кг и 19 коробок массой 61 кг каждая. Все эти коробки раскладывают по двум контейнерам. Пусть S - модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S:
a)если дополнительно требуется, что в контейнерах должно находится одинаковое количество коробок;
b)без дополнительного условия пункта a.
C6 Имеется 25 коробок массой 31 кг и 15 коробок массой 51 кг каждая. Все эти коробки раскладывают по двум контейнерам. Пусть S - модуль разности суммарных масс коробок в контейнерах. Найдите наименьшее значение S:
a)если дополнительно требуется, что в контейнерах должно находится одинаковое количество коробок;
b)без дополнительного условия пункта a.
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 5:29 AM | Сообщение # 21 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Немного фотографий КИМов (плохое качество):
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 6:45 AM | Сообщение # 22 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Еще фото варианта:
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 7:26 AM | Сообщение # 23 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Еще фото варианта:
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 10:14 AM | Сообщение # 24 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Еще фото КИМов:
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 10:15 AM | Сообщение # 25 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Еще фото КИМов:
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 10:16 AM | Сообщение # 26 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Еще фото КИМов:
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 10:37 AM | Сообщение # 27 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Еще фото КИМов:
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 11:04 AM | Сообщение # 28 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Еще фото КИМов:
|
| |
| |
| admin | Дата: Четверг, 2012-06-07, 11:04 AM | Сообщение # 29 |

Наблюдаю...
Группа: Администраторы
Сообщений: 631
Репутация: 26
Статус: Offline
Город: Москва
| Еще фото КИМов:
|
| |
| |
| tims72 | Дата: Четверг, 2012-06-07, 11:07 AM | Сообщение # 30 |

Студент
Группа: Пользователи
Сообщений: 46
Репутация: 6
Замечания: 0%
Статус: Offline
| При каком значении a выражение |6/x - 2| = ax - 1 на интервале от 0 до бесконеч. имеет более 2 корней
Сообщение отредактировал tims72 - Четверг, 2012-06-07, 11:13 AM |
| |
| |
|
|
|
