* ASCIIMath
`x^2+y_1+z_12^34` `d/dxf(x)=lim_(h->0)(f(x+h)-f(x))/h`
`[[a,b],[c,d]]((n),(k))`
`x/x={(1,if x!=0),(text{undefined},if x=0):}`
`hat(ab) bar(xy) ulA vec v dotx ddot y`
* LaTeXMath
$\diagup X\ind Y \tilde{A} \varnothing \R$
$A = \left(\begin{array}{c c c} 1-x & 0 & 0 \\ 0 & 1-x & 0 \\ 0 & 0 & 1-x \end{array}\right)$
$\sum a_i + \sum_{i=0}^{+\infty} b_i$
$f(x) = \left\{\begin{array}{l l} x^2 \sin \frac1x & \textrm{if } x \ne 0, \\ 0 & \textrm{if } x = 0 . \end{array}\right.$
$\displaystyle{ \lim_{x\to\infty} f(x) = k \choose r + \frac ab \sum_{n=1}^{+\infty} a_n + \left\{ \frac{1}{13} \sum_{n=1}^{+\infty} b_n \right\} }$
* AutoMath
amath
Example: Solving the quadratic equation.
Suppose a x^2+b x+c=0 and a!=0. We first divide by \a to get x^2+b/a x+c/a=0.
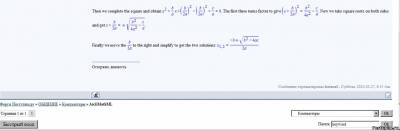
Then we complete the square and obtain x^2+b/a x+(b/(2a))^2-(b/(2a))^2+c/a=0. The first three terms factor to give (x+b/(2a))^2=(b^2)/(4a^2)-c/a. Now we take square roots on both sides and get x+b/(2a)=+-sqrt((b^2)/(4a^2)-c/a).
Finally we move the b/(2a) to the right and simplify to get the two solutions: x_(1,2)=(-b+-sqrt(b^2-4a c))/(2a)
endamath